如何理解递归查询在数据库管理中的作用与实现？

递归查询是一种计算机科学中的算法技术，它通过将问题分解为更小的子问题来解决问题，这些子问题与原始问题具有相同的形式。递归通常涉及函数自我调用，直到达到基本情况为止，此时问题可以直接解决而无需进一步递归。

（图片来源网络，侵删）

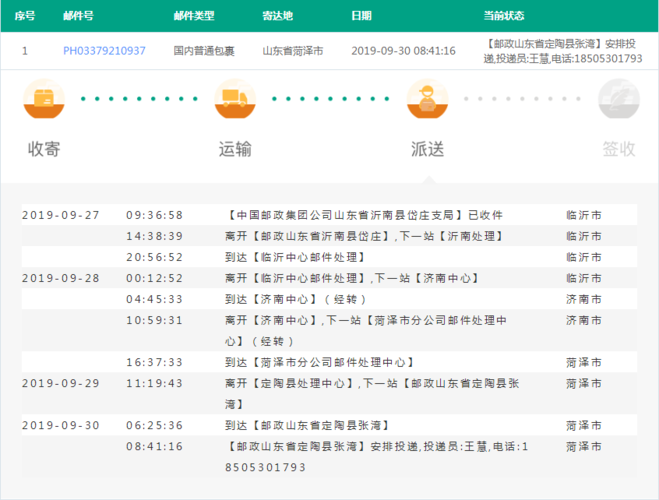
递归查询是一种在计算机科学和编程中常见的技术，它允许函数或算法调用自身来解决更小的问题实例，这种结构使得递归查询能够非常有效地解决一类可以通过重复将问题分解为更小的相同类型的子问题的问题，常见的递归问题包括计算阶乘、斐波那契数列、树的遍历等。

递归的基本概念

递归函数有两个基本要素：基本情况（base case）和递归情况（recursive case），基本情况是函数停止调用自身的条件，通常是最简单的问题实例；而递归情况则是函数继续调用自身来解决问题的情况。

示例：阶乘函数

def factorial(n):
    if n == 0:    # 基本情况
        return 1
    else:         # 递归情况
        return n * factorial(n1)

在这个例子中，当n等于0时，函数返回1，这是递归的终点，否则，函数会调用自身计算n1的阶乘，并将结果乘以n。

递归与迭代的比较

递归和迭代都是解决问题的方法，但它们在实现上有所不同，迭代使用循环来重复执行代码块，直到达到终止条件；而递归则通过函数调用自身来实现重复。

（图片来源网络，侵删）

迭代示例：阶乘函数

def factorial_iterative(n):
    result = 1
    for i in range(1, n+1):
        result *= i
    return result

这个迭代版本的阶乘函数使用了一个循环来计算结果，而不是通过函数调用自身。

递归的优点和缺点

优点：

简洁性： 递归可以将复杂的问题简化为简单的子问题，使得代码更加简洁易读。

自然性： 对于某些类型的问题，递归提供了一种自然的表达方式，如树的遍历。

分解能力： 递归能够将大问题分解为小问题，这在某些情况下可以提高效率。

（图片来源网络，侵删）

缺点：

性能开销： 递归函数调用会产生额外的开销，因为每次调用都需要保存状态。

栈溢出风险： 深度递归可能导致栈溢出错误，因为每个递归调用都会占用栈空间。

调试难度： 递归代码可能难以调试和维护，特别是对于初学者来说。

递归查询的应用

递归查询在多个领域都有应用，包括但不限于：

数据结构： 如二叉树的遍历（前序、中序、后序遍历）。

算法设计： 如快速排序、归并排序等。

数学问题： 如计算阶乘、斐波那契数列等。

编程语言： 许多编程语言支持递归，如Lisp、Prolog等。